W moich wcześniejszych wpisach kilkukrotnie odwoływałem się do kwantowej dystrybucji klucza (KDK), będącej jednym z głównych filarów kryptografii kwantowej. Miało to miejsce w kontekście omawiania takich zagadnień jak: kwantowa łączność satelitarna, internet kwantowy oraz bezpieczeństwo kryptowalut (wpisy: Kwantowa łączność satelitarna, Dwanaście technologii jutra i Kryptowaluty-Kwanty-Kosmos). Niniejszy wpis można potraktować jako uzupełnienie techniczne tych rozważań. Poniżej, przedstawię fizyczne podstawy na których opiera się kwantowa dystrybucja klucza oraz omówię, wprowadzony w 1984 roku, protokół Bennetta-Brassard BB84. Jest to najbardziej znany i historycznie pierwszy przykład protokołu KDK opartego na superpozycji kwantowej.  W późniejszych latach, wprowadzono także protokoły oparte na innych własnościach mechaniki kwantowej, m.in. na splątaniu kwantowym (np. protokół E91). Dyskusja szerokiego spektrum rozważanych obecnie protokołów kryptografii kwantowej wykracza poza ramy tego wpisu. Czytelnika zainteresowanego zapoznaniem się z pełniejszym obrazem tematu zachęcam do przestudiowania np. przeglądowego artykułu arXiv:1802.05517. Tytułem wstępu dodam jeszcze, że do zrozumienia niniejszego tekstu przydatna jest znajomość zasad mechaniki kwantowej. Niezapoznanego z nimi Czytelnika zachęcam do przestudiowania mojego wpisu Elementary quantum computing oraz znajdujących się w nim odnośników.

Zacznijmy więc. W największym skrócie, kwantowa dystrybucja klucza pozwala na, jak mówimy, bezwarunkowo bezpieczną wymianę klucza w oparciu o własności mechaniki kwantowej. To w jaki sposób fizyka mikroświata pozwala zapewnić “bezwarunkowe bezpieczeństwo”, postaram się wyjaśnić poniżej.  Jak to również zostanie dokładniej omówione w dalszej części tekstu, przepustowość wykorzystywanych do KDK tzw. kanałów kwantowych nie dorównuje tym osiąganym w klasycznych łączach światłowodowych oraz radiowych. Z tego też powodu, łącza kwantowe wykorzystywane są obecnie do przesyłania sekretnych kluczy, pozwalających zaszyfrować (klasyczną) wiadomość, nie zaś do transmisji samej wrażliwej informacji.  Udostępniony, za pośrednictwem KDK, klucz może być wykorzystany do zaszyfrowania danych np. z użyciem bardzo silnego symetrycznego szyfru AES 256.  Przykładową architekturę systemu do kwantowej dystrybucji klucza, zawierającą zarówno kanał kwantowy (do przesyłania klucza) oraz kanał klasyczny (do przesyłania zaszyfrowanych danych oraz informacji pomocniczych), przedstawia rysunek poniżej:

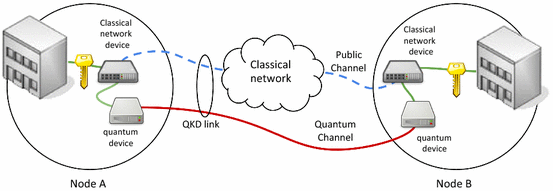
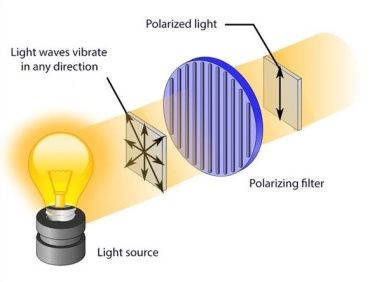
W przypadku kanału klasycznego opartego o łącze światłowodowe, zaszyfrowana informacja przesyłana jest za pomocą światła. Do przesłania klucza poprzez kanał kwantowy również wykorzystywane jest pole elektromagnetyczne. Z tą jednak różnicą, że odbywa się to za pośrednictwem nie klasycznych impulsów  lecz pojedynczych kwantów światła, czyli fotonów. Do zakodowania informacji kwantowej wykorzystywane są zaś stany polaryzacji światła. Przedyskutujmy to bardziej szczegółowo. Mianowicie, światło docierające do nas, na przykład, ze Słońca lub z żarówki nie jest spolaryzowane. Na poziomie klasycznym,  oznacza to, że światło tego typu składa się z fal elektromagnetycznych oscylujących jednakowo we wszystkich kierunkach  prostopadłych do osi propagacji światła.  Żeby dokonać selekcji fal elektromagnetycznych, których wektor natężenia pola oscyluje w wybranym przez nas kierunku, stosujemy polaryzator. Przepuszczając niespolaryzowane światło przez polaryzator liniowy dokonujemy jego polaryzacji.  Jeśli za polaryzatorem liniowym umieścilibyśmy kolejny podobny polaryzator, jednakże z osią polaryzacji ustawioną prostopadle do tej pierwszej, dokonalibyśmy całkowitego wygaszenia światła. Zachęcam do przeprowadzenia tego prostego eksperymentu np. pozyskując dwa polaryzatory liniowe z powierzchni wyświetlaczy ciekłokrystalicznych zepsutego zegarka lub kalkulatorka.

Zgodnie z regułą dodawania wektorów,  każdą falę elektromagnetyczną można zapisać jako sumę dwóch fal elektromagnetycznych, prostopadłych do siebie w płaszczyźnie polaryzacji. Czyli inaczej, każdą polaryzację liniową światła można opisać jako superpozycję dwóch normalnych względem siebie polaryzacji, nazwijmy je horyzontalną H (ang. horizontal) oraz wertykalną V (ang. vertical).

Przeprowadźmy teraz następujący eksperyment myślowy. Załóżmy, że dysponujemy źródłem światła niespolaryzowanego oraz zestawem płytek półprzepuszczalnych tłumiących światło. Ustawiające je kolejno na osi optycznej, możemy doprowadzić do sytuacji w której  przez zestaw płytek przedostawać się będą jedynie pojedyncze fotony. Możemy w tym miejscu zapytać co się stanie gdy pojedynczy foton napotka polaryzator światła?  Okazuje się, że foton taki z pewnym prawdopodobieństwem może przejść przez polaryzator, jak również z pewnym prawdopodobieństwem może zostać przez niego zatrzymany. Jest to konsekwencją kwantowej natury fotonu, co przejawia się istnieniem fotonu w stanie kwantowym , będącym superpozycją kwantową dwóch polaryzacji, co zapisujemy jako:

,

tak, że . Prawdopodobieństwo znalezienia fotonu w stanie równe jest , natomiast prawdopodobieństwo znalezienia fotonu w stanie równe jest . Stany bazowe i odpowiadają dwóm prostopadłym względem siebie polaryzacjom. Tak więc, polaryzacja światła ma swoje źródło na poziomie pojedynczych fotonów i związana jest z tym, że są one bezmasowymi bozonami o spinie 1. Dla cząstek takich istnieją dwa możliwe rzuty wektora momentu pędu na kierunek jego propagacji. Te dwa stany tak zwanej skrętności (ang. helicity) fotonów, na poziomie klasycznym, odpowiadają dwóm możliwym polaryzacjom kołowym światła (lewoskrętnej i prawoskrętnej). Stany o polaryzacji lewoskrętnej i prawoskrętnej są superpozycjami stanów o polaryzacji liniowej:

    oraz   .

Fakt, że foton jest opisywany przez kwantową superpozycję dwóch stanów bazowych, czyli jego stan należy do dwuwymiarowej przestrzeni Hilberta ma ogromne znaczenie z punktu widzenia kwantowej teorii informacji. A mianowicie, foton może być wykorzystany jako nośnik najmniejszej porcji informacji kwantowej, tak zwanego kubitu. Z tego też powodu możemy utożsamić stany polaryzacji fotonu ze stanami bazowymi kubitu: oraz . Oznaczmy tę bazę jako .

Do przeprowadzenia kwantowej dystrybucji klucza, w ramach protokołu BB84, będziemy potrzebowali wprowadzić jeszcze jedną bazę. Mianowicie, , gdzie stany bazowe wyrażają się jako  następujące superpozycje:

   oraz    .

Jeśli stany bazowe i opisują stany polaryzacji pod kątami odpowiednio i to stany polaryzacji i opisują polaryzacje liniowe odpowiednio pod kątami   i . Warto w tym miejscu również zaznaczyć, że stany i są stanami własnymi operatora do wartości własnych i odpowiednio. Natomiast, stany i są stanami własnymi operatora odpowiednio do wartości własnych  i (operatory i odpowiadają macierzom Pauliego  i ). Wszystkie z wprowadzonych tu stanów bazowych można wytworzyć przepuszczając foton przez polaryzator liniowy ustawiony pod jednym z czterech kątów. Ponadto, powyższy dobór baz nie jest przypadkowy i wynika z faktu, że bazy i są przykładem tak zwanych wzajemnie nieobciążonych baz (ang. mutually unbiased bases), spełniających warunek:

,

gdzie a . Oznacza to, że bazy te wykluczają się w sposób maksymalny, uniemożliwiając jednoczesne wykonywanie pomiarów na kubicie w obydwu bazach. W przypadku fotonu ma to następujące konsekwencje: Jeśli przygotujemy foton np. w stanie bazowym i przepuścimy go przez analizator polaryzacji pod kątami  i (odpowiadających stanom polaryzacji bazy ), to po przejściu przez taki analizator nie nastąpi zmiana stanu fotonu. Jednakże, jeśli na drodze tego samego fotony umieścimy analizator polaryzacji pod kątami  i (odpowiadających stanom polaryzacji bazy ), to po przejściu przez taki analizator foton  z prawdopodobieństwem znajdzie się w stanie o polaryzacji  i z takim samym prawdopodobieństwem w stanie o polaryzacji   .  Jeśli foton ten będziemy chcieli zaś ostatecznie przeanalizować wykorzystując analizator ze stanami polaryzacji odpowiadającymi bazie to z prawdopodobieństwem zaobserwujemy ten foton w stanie  i z prawdopodobieństwem w stanie (taki sam wynik uzyskalibyśmy jeśli foton byłbym przygotowany w stanie ). Próba przeanalizowania stanu fotonu we wzajemnie obciążonej bazie wprowadza więc maksymalną niepewność co do stanu początkowego.  Własność  ta znajduje bezpośrednie zastosowanie w protokole BB84.

Przyjdźmy więc do jego omówienia. Rozważamy nadawcę (A) i odbiorcę (B) których zwyczajowo określamy mianem Alicji i Boba.  Alicja ma za zadanie przesłać do Boba klucz (ciąg bitów) wykorzystując stany polaryzacji fotonu. Ma ona do dyspozycji 4 stany polaryzacji fotonu odpowiadające stanom bazowym baz i . Klucz stanowi losowy ciąg binarny i  , który można wygenerować np. wykorzystując kwantowy generator liczb losowych (z artykułu arXiv:1405.0453 można dowiedzieć się jak samemu zbudować taki generator w oparciu o smartfon). Alicja wprowadza następujące kodowanie klasycznych bitów klucza za pomocą kwantowych stanów  polaryzacji fotonu. Mianowicie, stany polaryzacji i kodują , natomiast stany polaryzacji i kodują . W praktyce, generacja klucza odbywa się przez losowe ustalanie jednej z czterech pozycji polaryzatora Alicji (rysunek poniżej).

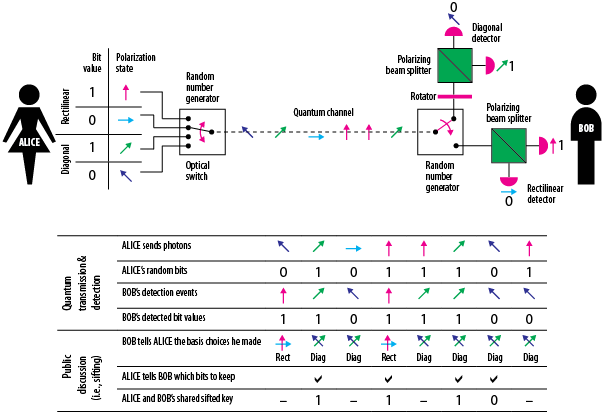
Przesyłane od Alicji spolaryzowane fotony Bob będzie rejestrował za pomocą analizatora który może przyjmować takie same orientacje jak polaryzator Alicji. Stany polaryzatora Alicji nie są publiczne, Bob będzie więc dokonywał analizy polaryzacji fotonów w (wybieranych losowo) bazach i .  Na podstawie swoich pomiarów, odzyska on pewien ciąg bitów. Następnym krokiem jest publiczne ogłoszenie przez Boba stanów analizatora (baz) w których dokonywał on kolejnych pomiarów. Warto tu podkreślić, że oczywiście nie upublicznia on samych wyników pomiarów. W ramach danej bazy możliwe są wciąż dwie wartości bitu, wartość klucza pozostaje więc ukryta. Następuje teraz tak zwane uzgodnienie baz (ang. basis reconciliation). Mianowicie, Alicja informuje Boba które użyte przez niego bazy są zgodne ze stanami polaryzacji w których przygotowała ona sekretny klucz. Zdekodowane przez Boba, dla uzgodnionych baz, wartości bitów stanowią sekretny klucz. Ostatnim etapem protokołu jest zweryfikowanie czy nie nastąpiła próba “podsłuchania” przesyłanych kanałem kwantowym informacji.

Omówienie tej kwestii zacznijmy od wyartykułowania jednej z fundamentalnych własności mechaniki kwantowej. Mianowicie, nie jest możliwe idealne skopiowanie nieznanego stanu kwantowego. Nie jest więc możliwe “podłączenie się” do kanału kwantowego i skopiowanie przesyłanej informacji.  Własność ta jest ucieleśniona w twierdzeniu o zakazie klonowania, którego dowód dla przypadku kubitów przedstawiam poniżej.

Twierdzenie o zakazie klonowania (ang. no-cloning theorem) leży u podstaw bezwarunkowego bezpieczeństwa protokołów kryptografii kwantowej. Mówi ono, że nie jest możliwe wykonanie dokładnej kopii (klonu) nieznanego stanu kwantowego. Sformułowanie tego twierdzenia zawdzięczamy Williamowi Woottersowi oraz Wojciechowi Żurkowi [Ref]. Poniżej przedstawię jego dowód, dla przypadku stanu kubitu.

Rozważmy stan kwantowy . Naszym celem będzie próba skopiowania tego stanu, czyli chcemy aby pewien inny stan, nazwijmy go  , przetransformować (“nadpisać”) w stan , nie zmieniając jednocześnie stanu  . Rozważamy więc wyjściowo stan będący następujacym iloczynem tensorowym:  . Ponadto, wprowadźmy (unitarny) operator kopiujący, nazwijmy go  , którego działanie  powinno być następujące: , dla dowolnego stanu . Żeby sprawdzić czy jest to możliwe, zadziałajmy najpierw operatorem na stany bazowe  i . Działanie operatora powinno dawać  oraz .  Zakładając, że powyższe jest spełnione, spróbujmy przeprowadzić kopiowanie stanu . Skorzystamy w tym miejscu z własności liniowości operatorów rozważanych w mechanice kwantowej (czyli np. , dla dowolnych stanów i ). W konsekwencji, otrzymujemy:

.

Stan końcowy  jakiego jednak oczekiwalibyśmy w wyniku kopiowania (klonowania) to:

,

który jest odzyskiwany tylko w szczególnych przypadkach stanów bazowych,  tzn. kiedy  i lub i  . Powyższa analiza dowodzi tego, że nie jest możliwe skopiowanie nieznanego stanu kubitu. Przeprowadzenie dowodu dla przypadku dowolnego stanu pozostawiam Czytelnikowi jako ćwiczenie.

Pomimo zakazu klonowania stanów kwantowych, istnieją pewne strategie ataków na protokoły kryptografii kwantowej. Np. podsłuchujący (nazwijmy ją Ewa) może ustawić na drodze optycznej fotonu analizator i próbować odczytać pewne bity klucza. Jak to już jednak dyskutowaliśmy powyżej, obecność takiego analizatora w sposób nieodłączny wiąże się z wpłynięciem na stany fotonu. W celu wyeliminowania możliwości podsłuchu, Alicja i Bob porównują publicznie część klucza. Jeśli w wybranym ciągu bitów nie zauważą różnić, mają pewność, że nie nastąpiła próba ataku. Oczywiście, w praktyce mogą występować pewne różnice w ciągu bitów wynikające z występowaniem szumu, generującego pewien poziom błędów. Istnieje jednak metoda dokładnego określenia jaki poziom niezgodności porównywanego ciągu bitów jest dopuszczalny dla zachowania poufności wymiany klucza. Metoda ta opiera się na wykorzystaniu teorii informacji i pozwolę sobie zarysować jej uproszczoną postać. Zacznijmy od odpowiedzi na pytanie jak dużo błędów do odczytywanego przez Boba ciągu bitów będzie wprowadzał ustawiony przez Ewę, na drodze fotonu, analizator. Analizator ten może być dostosowany do bazy lub .  Prosta probabilistyka mówi nam, że prawdopodobieństwo nie zaburzenia przez Ewę pojedynczego bitu przesyłanego klucza wynosi:

.

Czyli, starająca się wykraść sekretny klucz Ewa, w 25 % przypadków wprowadzi błąd do przesyłanego ciągu bitów. Ponadto, ponieważ z prawdopodobieństwem analizuje ona foton we właściwej bazie, z takim też prawdopodobieństwem odczyta ona poprawnie wartość przesyłanego bitu. Ponieważ, wyjściowo, nie zna ona ustawień polaryzatora Alicji, nie jest ona jednak w stanie stwierdzić który bit odczytała prawidłowo a który nie. Odkodowania połowy przesyłanych bitów klucza może dokonać jedynie poznawszy (post factum) ustawienia polaryzatora Alicji. Może to więc zrobić dla bitów dla których następuje sprawdzenie klucza przez Alicję i Boba.

Do skwantyfikowania ilości błędów wprowadzanych podczas kwantowej transmisji informacji używa się wielkości zwanej QBER (Quantum Bit Error Rate) – która zdefiniowana jest jako stosunek liczby kubitów z błędem () względem całkowitej liczby przesyłanych kubitów :

.

Jeśli przez oznaczymy część kubitów analizowanych przez Ewę, to wprowadzany przez Nią QBER wynosi , gdzie czynnik wynika z przeprowadzonych powyżej rozważań probabilistycznych. Przywołajmy teraz pojęcie informacji wzajemnej (ang. mutual information), która pozwoli nam skwantyfikować jaka część informacji jest tracona w kanale kwantowym w wyniku ataków Ewy. Jak można pokazać, wzajemna informacja pomiędzy Alicją a Bobem wyraża się jako

,  gdzie

to tak zwana entropia informacyjna Shannona. Wzajemna informacja pomiędzy Alicją a Ewą wynosi zaś

,

co wynika z faktu, iż Ewa (znając położenie polaryzatorów Ewy) jest w stanie teoretycznie odzyskać wartości połowy “podsłuchiwanych” przez Nią bitów. Jeśli informacja w układzie Alicja-Ewa zaczyna być większa niż pomiędzy Alicją i Bobem , przesyłanie klucza przestaje być bezpieczne. Na tej podstawie, rozpatrując warunek graniczny , otrzymujemy, że (przy powyższych założeniach) bezpieczeństwo kwantowej dystrybucji klucza zapewnione jest jeśli poziom błędów jest mniejszy niż około . Jeśli, porównując wybrane bity klucza, Alicja i Bob zanotują różnicę na wyższym poziomie, nie można zaakceptować przesyłanego klucza  i należy powtórzyć całą procedurę.   

Przeprowadzona powyżej analiza ma znaczenie praktyczne i znajduje zastosowanie w istniejących systemach do kwantowej dystrybucji klucza. Na rynku istnienie obecnie kilka zestawów które pozwalają przeprowadzić KDK wykorzystując protokoły oparte na superpozycji kwantowej. Na rysunku poniżej przedstawiono przykładowy zestaw wykorzystujący zmodyfikowaną wersję protokołu BB84, tzw. protokół T12. 

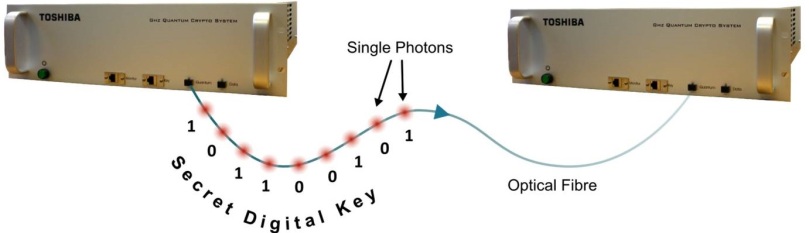
Do przesyłania fotonów, dostępne komercyjnie systemy kryptografii kwantowej stosują światłowody. Niepożądaną cechą takiego rozwiązania jest jednak wykładnicze tłumienie natężenia światła w funkcji przebytego przez światło dystansu. Z uwagi na twierdzenie o zakazie klonowania oraz na fakt posługiwania się w kwantowej dystrybucji klucza pojedynczymi fotonami, nie jest możliwe stosowanie klasycznych wzmacniaczy sygnału.  Dlatego też, kwantowa dystrybucja klucza za pośrednictwem światłowodów jest dzisiaj ograniczona do odległości poniżej około 400 km.

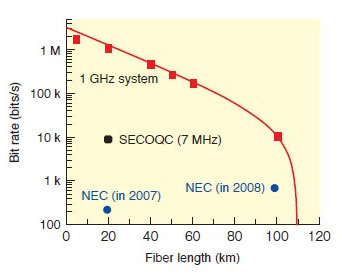
Wraz z długością linii transmisyjnej spada jej przepustowość.  Na bardzo krótkich dystansach osiągane są obecnie wartości około 10 Mb/s (arXiv:1807.04484). Na odległościach rzędu 50 km wartość ta spada już do około 1 Mb/s. Natomiast, nieubłagana natura zaniku eksponencjalnego sprawia, że na dystansach około 400 km KDK można przeprowadzać w tempie jedynie około 1 bitu na sekundę (co jest wielkością niepraktyczną).

Możliwym rozwiązaniem dla powyższych trudności jest stosowanie powielaczy kwantowych (ang. quantum repeater). Są to jednakże bardzo złożone systemy, będące wciąż w fazie badań.  Dużo bardziej obiecującym rozwiązaniem jest wykorzystanie faktu jedynie odwrotnego z kwadratem odległości zaniku natężenia światła w próżni, oraz dużo słabszego niż w ciele stałym tłumienia fotonów w gazach. Rozwiązanie to wiąże się z wykorzystaniem przestrzeni kosmicznej do przeprowadzenia kwantowej dystrybucji klucza. Możliwość taka została pomyślnie potwierdzona eksperymentalnie na skalach międzykontynentalnych w 2017 roku z wykorzystaniem protokołu BB84. Zagadnienie to opisuję bardziej szczegółowo we wpisie Kwantowa łączność satelitarna.

© Jakub Mielczarek