Every piece of information we deal with daily can be distilled into a sequence of just two distinct symbols, mirroring the elegant code of dots and dashes in the Morse alphabet. This unveils a profound parallel between the structure of information and that of matter—both possess a foundational granularity. The “elementary particle of information” is aptly named a “bit.”
The universally acknowledged symbols for these fundamental bits are 0 and 1, encapsulating the binary essence of information. In particular, we can represent any natural number as a finite binary sequence. Consequently, the inception year of the Jagiellonian University, etched indelibly into memory, materializes as 010101010100—a rhythmic amalgamation of five alternating 01s and 00s.
Interestingly, the concept of encoding not only natural numbers but also fractional quantities in a similar manner was a revelation that predates modern times. Ancient Egypt stands as a testament to this foresight. However, the purview of encoding extends beyond numerical constructs; it embraces the entire spectrum of human expression, encompassing alphabets, special characters, intricate images, and an array of information’s myriad forms.
Information, by its very nature, seldom remains stagnant but is subject to constant metamorphosis, which, by means of the representation of bits as electrical impulses, is conducted by computers. Computers, in turn, are nothing more than certain physical systems.
Following this line of thought, we can come to the conclusion that, basically, every piece of reality is a computer of some kind, processing or at least storing a certain type of information. But is this really the case? Does every physical process correspond to an information processing that a computer could handle? This contemplation unfurls into a grander query: is the totality of our reality computable?
An attempt to confront these ostensibly philosophical questions was made in the 1930s by a British mathematician, cryptologist, and decidedly versatile genius Alan Turing. Analyzing the problem of computability of various problems, he introduced an abstract model of a computing machine—an idea subsequently christened the Turing machine in his honor. The Turing machine stands as a conceptualization of an “imaginary mathematician” meticulously carrying out the step-by-step processing of information, which is represented as a binary string adorning an infinitely extensive tape.
Though it might appear astonishing, every operation executed by contemporary computers can be replicated using a construct as rudimentary as a Turing machine that can actually be built, for example, from LEGO bricks.

While this particular construct does not offer an optimal method for information processing, contemplations surrounding it have yielded profound insight into the boundaries of computability. Notably, building upon Turing’s ideas, American mathematician Alonzo Church articulated a conjecture that, in one of its incarnations, can be framed thus: Any form of computation—pertaining to the manipulation of information—executed by a physical system (i.e., one that obeys the laws of physics) can be emulated by a Turing machine.
The Church-Turing hypothesis, as it is dubbed, holds profound significance in the context of simulating physical processes. Processes that can be represented through operations executable on a Turing machine are bestowed with the epithet of being “complete in the Turing sense.” The question of whether the entirety of physical phenomena can be encapsulated within such completeness, and by extension, whether the entire Universe is encompassed by this Turing-style completeness, stands as an unresolved enigma.
To date, no counterexample has emerged to challenge the Church-Turing hypothesis, yet the certainty eludes us. It is essential to emphasize that the completeness of the Universe in this framework implies that certain problems—known to be incomplete in the Turing sense—forever reside beyond the realm of solution.
The pursuit of an answer to the profound question regarding the completeness of the Universe within the framework of Turing’s conception is further compounded by the intricate adjustments necessary when entering the atomic realm. Here, the familiar encoding of information as binary sequences faces a fundamental rethinking. In the microcosmic domain governed by the intricate laws of quantum mechanics, classical information theory gracefully evolves into the realm known as quantum information theory.
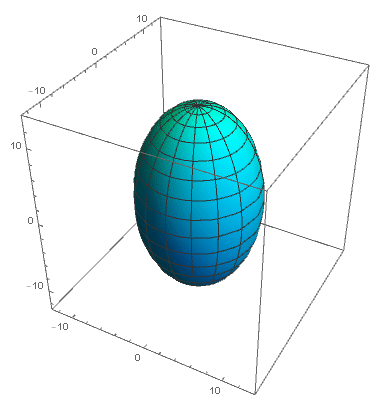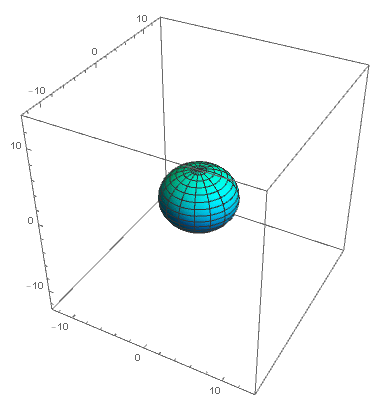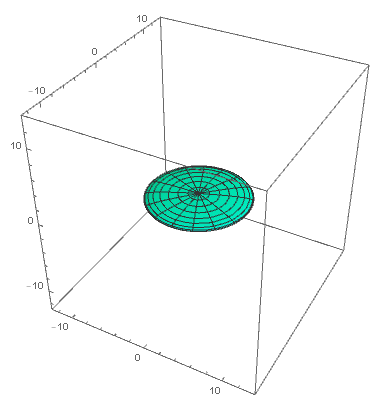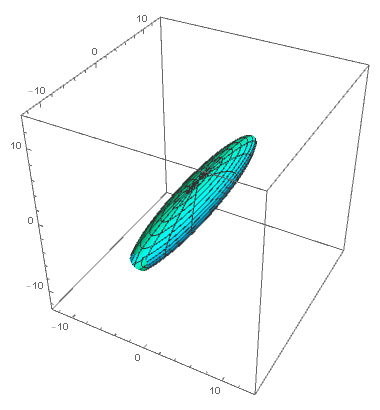
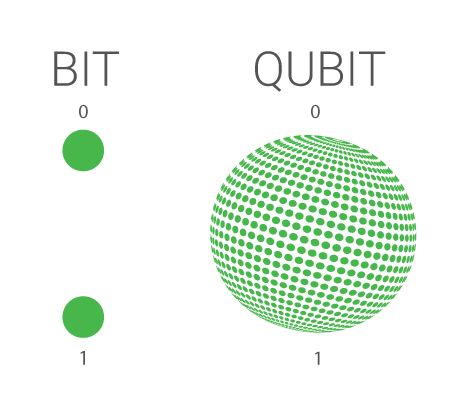
Within this novel landscape, the very building block of information transforms from the conventional bit to the quantum variant—the qubit. Visualizing a qubit as a spherical canvas akin to Earth, where the poles host the familiar classical bit values of 0 and 1, we gain a glimpse into its essence. However, a qubit can “live” not only at the poles but at any other point, of which there are infinitely many on the sphere (which we call the Bloch sphere). On this sphere, each point represents a unique quantum superposition of the classical values 0 and 1, painting a vivid portrait of quantum possibility.
However, this narrative of quantum complexity does not halt there. The states of more intricate quantum systems are not confined to fixed bit sequences like 011. Instead, their depiction transcends such simplicity and embraces the entwined concept of superposition. Imagine these states as harmonious amalgamations of every feasible sequence of bits for a given length. In practical terms, this encompasses permutations like 000, 001, 010, 100, 011, 101, 110, and 111. The symphony of quantum states expands to include a diverse ensemble of possibilities. For a quantum system described by n qubits, its quantum state proliferates into a superposition of 2n binary strings, each boasting a length of n bits.

Quantum information processing is, to some extent, possible with classical computers and, therefore, with a Turing machine. Nonetheless, this endeavor is, in broad terms, an arduous endeavor. This is primarily due to the fact that for a quantum system comprised of n qubits, the undertaking necessitates the manipulation of 2n probability amplitudes. Each of these amplitudes corresponds to one of the feasible n-bit strings. Notably, every one of these amplitudes corresponds to a so-called complex number (composed of two real numbers), which can be represented by a sequence of bits. The length of this sequence burgeons in proportion to the precision sought in the calculation.
Hence, for even a modestly sized quantum system of, say, a hundred qubits, the challenge becomes monumental. To be precise, operations on 2100 = 1267650600228229401496703205376 probability amplitudes are requisite. This prodigious magnitude exceeds the capabilities of existing classical computers and even defies the bounds of conceivable future classical computing innovations.
Hence, attempting to simulate the intricate realm of quantum reality using a classical computational device is profoundly inefficient. A solution to this conundrum emerges through the extension of the Turing machine into the quantum domain, culminating in the model of a universal quantum computer.
The idea of such quantum computational frameworks traces back to the early 1980s, thanks to the pioneering work of physicists Paul Benioff and David Deutsch. Almost simultaneously, a luminary in the world of physics—Richard Feynman—proposed that any discrete quantum system can be simulated in an exact way (can be “imitated”) by means of operations performed on a quantum computer. Following this train of thought, if the Universe can be distilled into a finite arrangement of qubits, it would resonate with the completeness in the sense of the quantum Turing machine. In essence, the Universe could then serve as an example of a universal quantum computer, with the intricate dance of qubits orchestrating the fabric of existence.
Does the Universe, in reality, embody an immense quantum computer engaged in ceaseless quantum information processing? At this moment, this remains an enigma that eludes our grasp. However, our current comprehension of fundamental physics—at the very limit of our knowledge and imaginative capacity—does not preclude this intriguing possibility.
This boundary of our cognitive horizon is demarcated by the Planck scale, a realm where our understanding of physics encounters its utmost frontier. In this uncharted territory, a diverse array of quantum theories of gravity emerge as contenders, each offering a distinct portrayal of the quantum intricacies underpinning space and time.
Among these contenders, one theory stands prominently—the loop quantum gravity. Introduced in the early 1990s by Abhay Ashtekar, Carlo Rovelli, and Lee Smolin, this theory envisages a granular structure of space at the Planck scale—an architecture fundamentally discrete, resembling the concept of atoms in a quantum realm. This theory nurtures the possibility of simulating this quantum fabric, aligning with the essence of Feynman’s visionary ideas.
For over a decade, I have been pondering the feasibility of distilling loop quantum gravity into a system governed by qubits—a crucial step that could pave the way for the realm of quantum simulations. Yet, it was only in 2017 that I mustered the determination to propel this idea from the realm of theory into the realm of reality. This surge of initiative was catalyzed by a significant turning point: the debut of the first quantum computers, wielding the power of a handful to a dozen qubits.
In the course of the research we are currently conducting as part of the Quantum Cosmos Lab team operating at the Institute of Theoretical Physics at the Jagiellonian University, we have managed not only to theoretically demonstrate the possibility of running quantum simulations of models of the Universe described by loop quantum gravity but also to perform the first quantum simulations of this type.
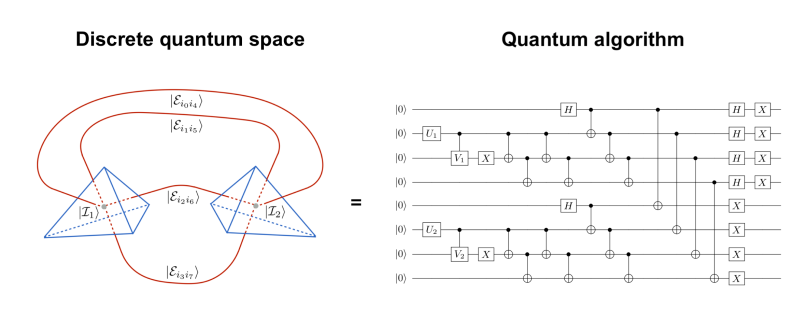
The simulations we are conducting, constrained by the nascent capabilities of current quantum computers, remain in their rudimentary stages, employing at most a dozen “raw” qubits. Despite these limitations, these initial attempts enable us to sculpt configurations that paint a portrait of a homogeneous quantum universe model.
With the development of quantum computing engineering, we will be able to add more and more embellishments to this microscopic universe. Forecasts beckon a promising trajectory: in the coming five years, we anticipate reaching a level of simulation performance that surpasses the reach of contemporary classical supercomputers. The use of a classical Turing machine will still remain theoretically possible, but its extreme inefficiency renders it unfeasible in practice. Thus, while the development of quantum simulations ushers in an era of uncharted potential, it is essential to recognize that the resulting quantum emulation of the cosmos remains, at this juncture, a nascent quantum embryo—a reflection of the universe we inhabit, yet still in a very early stage of its evolution.
Looking thousands of years into an uncertain future, we find ourselves unable to definitively dismiss the prospect that comprehensive simulations of sizable portions of the Universe might eventually materialize. Yet, it remains an immutable truth that no simulation, no matter how advanced, can ever encapsulate the entirety of the Universe that envelopes us. Unless, of course, in the hypothetical limiting case when it would be used to simulate itself as a whole. Yet, this transcendental eventuality strays from the realm of simulation into the territory of reality. This theoretical juncture transforms the simulation into what we call “reality”— being complete in the Turing sense.
Bibliography
[1] J. Mielczarek, Prelude to Simulations of Loop Quantum Gravity on Adiabatic Quantum Computers,’ Front. Astron. Space Sci. 8 (2021), 95
[2] J. Mielczarek, Spin Foam Vertex Amplitudes on Quantum Computer – Preliminary Results, Universe 5 (2019) no.8, 179.
[3] G. Czelusta, J. Mielczarek, Quantum simulations of a qubit of space, Phys. Rev. D 103 (2021) no.4, 046001.
© Jakub Mielczarek