Jednym z najważniejszych filarów bezpieczeństwa w cyberprzestrzeni jest kryptografia. Z punktu widzenia jednostki, m.in. to dzięki kryptografii możliwe jest korzystanie z systemów bankowości elektronicznej, dokonywanie zakupów online, zachowanie prywatności w komunikacji internetowej, czy też zapewnienie poufności naszej dokumentacji medycznej w medycznych systemach teleinformatycznych.   Z punktu widzenia Państwa, kryptografia to zaś kluczowy element tarczy chroniącej przed cyberatakami na strategiczne komponenty (zarówno infrastrukturę fizyczną, jak i zasoby cyfrowe) oraz narzędzie umożliwiające wymianę i przechowywanie informacji niejawnej, o podstawowym znaczeniu dla interesu i bezpieczeństwa Państwa.

Rozwój technologii kwantowych, opartych na niezwykłych własnościach mikroświata, ma z punktu widzenia cyberbezpieczeństwa znaczenie dwojakie. Z jednej strony, kwantowe przetwarzanie informacji dostarcza nowej metody prowadzenia ataków na klasyczne systemy kryptograficzne, poprzez tzw. kryptoanalizę kwantową. Państwa lub organizacje, które wejdą w posiadanie zaawansowanych systemów umożliwiających prowadzenie obliczeń kwantowych będą więc dysponowały nowym narzędziem stanowiącym potencjalne zagrożenie dla cyberbezpieczeństwa. Z drugiej zaś strony, technologie kwantowe dostarczają zupełnie nowych rozwiązań kryptograficznych, które mogą pozwolić osiągnąć poziom bezpieczeństwa w wymianie i magazynowaniu informacji, niedostępny z wykorzystaniem kryptografii klasycznej. W szczególności, rozwiązania takie mogą uchronić przed atakami z wykorzystaniem kryptoanalizy kwantowej.    

To czy technologie kwantowe ostatecznie obniżą poziom cyberbezpieczeństwa, czy też tylko go wzmocnią, zależy zarówno od tempa i zakresu postępów w rozwoju technologii kwantowych oraz decyzji państw i organizacji międzynarodowych w zakresie wdrażania rozwiązań odpornych na kryptoanalizę kwantową [1].  Z uwagi na wysokie koszty oraz unikalną wiedzę i doświadczenie, które są niezbędne do rozwoju technologii kwantowych, realne są scenariusze w których zarówno zabezpieczenie cyberprzestrzeni przed atakami, jak i wejście w posiadanie kwantowych narzędzi kryptoanalitycznych, będzie postępowało bardzo niejednorodnie. Stanowić to więc może realne zagrożenie dla krajów nie należących do światowej czołówki w obszarze nauki i techniki.

Kryptoanaliza kwantowa

Zagrożenie związane z kryptoanalizą kwantową wynika z możliwości redukcji tak zwanej złożoności obliczeniowej problemów, na których opierają się algorytmy kryptografii klasycznej. Wiąże się to z występowaniem paralelizmu kwantowego (Dodatek A), który jest możliwy do zrealizowania poprzez wykonanie algorytmów kwantowych na odpowiednio zaawansowanych komputerach kwantowych.  Kwantowa redukcja złożoności jest teoretycznie możliwa zarówno w przypadku kryptografii symetrycznej (z tajnym kluczem), jak i kryptografii asymetrycznej (z kluczem publicznym). Otrzymywany, dzięki algorytmom kwantowym, stopień redukcji złożoności jest jednak zasadniczo różny dla tych dwóch przypadków.  W konsekwencji, niektóre stosowane obecnie algorytmy kryptografii symetrycznej pozostaną niepodatne na kryptoanalizę kwantową. Natomiast, np. wykorzystywane powszechnie w bankowości elektronicznej,  systemach płatniczych, czy też  rozwiązaniach opartych o technologię Blockchain, algorytmy kryptografii asymetrycznej zostaną wystawione na potencjalne zagrożenie.

Przedyskutujmy powyższą kwestię bardziej szczegółowo. W przypadku kryptografii symetrycznej, siła zabezpieczenia opiera się, w dużej mierze, na wielkości przestrzeni tajnego  klucza. Przykładowo, dla stosowanego powszechnie  algorytmu symetrycznego AES (Advanced Encryption Standard) z kluczem 256 bitowym, przestrzeń klucza posiada N = 2²⁵⁶ elementów, co jest w przybliżeniu równe jeden i 77 zer. Przeszukanie tak ogromnego zbioru w poszukiwaniu tajnego klucza jest praktycznie niemożliwe, zarówno korzystając z obecnych, jak i możliwych do przewidzenia przyszłych zasobów obliczeniowych.

Zastosowanie algorytmów kwantowych pozwoli przyśpieszyć proces poszukiwania przestrzeni klucza w ataku siłowym (ang. brute force). Mianowicie, jak pokazał w 1996 roku Lov Grover, wykorzystanie obliczeń kwantowych pozwala zredukować średnią ilość prób potrzebnych do znalezienia elementu w nieuporządkowanym N elementowym zbiorze z N/2 do pierwiastka kwadratowego z N, czyli N^1/2. Oznacza to, że w przypadku AES-256, komputer kwantowy będzie wciąż potrzebował wykonać około N^1/2=2¹²⁸ prób w celu znalezienia tajnego klucza. Nawet więc dysponując komputerem kwantowym, na którym zaimplementowany mógłby zostać algorytm Grover’a, siła szyfru pozostanie na poziomie porównywalnym z AES z kluczem 128 bitowym. Jest to zabezpieczenie zupełnie wystarczający dla większości standardowych sytuacji.

Rzecz ma się jednak inaczej w przypadku szyfrów kryptografii asymetrycznej (z kluczem publicznym). Istota kryptografii asymetrycznej opiera się na trudności  obliczeniowej pewnych operacji matematycznych, dla których zaś operacja „przeciwna” jest łatwa do przeprowadzenia. Do najbardziej znanych przykładów algorytmów tego typu zaliczają się DH (Diffie-Hellman), RSA (Rivest-Shamir-Adleman) oraz ECC (Elliptic Curve Cryptography). Algorytm DH jest oryginalnie pierwszą propozycją kryptografii z kluczem publicznym a trudnym problemem jest tutaj znajdowanie tak zwanego logarytmu dyskretnego (logarytmu określonego na skończonym zbiorze liczb). Z kolei, popularny algorytm RSA wykorzystuje złożoność obliczeniową rozkładu liczby na czynniki pierwsze (zagadnienie faktoryzacji). Wadą algorytmów DH i RSA jest konieczność stosowania stosunkowo długich kluczy (obecnie powszechnie stosuje się klucze 2048 bitowe). Problem ten rozwiązuje zastosowanie algorytmów ECC, wykorzystujących problem złożoności logarytmu dyskretnego dla działania zdefiniowanego na krzywej eliptycznej. Poziom bezpieczeństwa porównywalny z DH lub RSA z kluczem 2048 bitwym otrzymamy stosując algorytm ECC z kluczem 224 bitowym. Między innymi z tego powodu, algorytmy ECC znalazły szerokie zastosowanie w technologii Blockchain.

Okazuje się, że trudność obliczeniową na której oparte są przytoczone powyżej algorytmy kryptografii asymetrycznej można sprowadzić do zagadnienia znalezienia okresu pewnej funkcji. O ile jednak, znajdowanie okresu funkcji jest z perspektywy komputerów klasycznych zadaniem trudym obliczeniowo, nie jest już takim dla komputerów kwantowych. Mianowicie, jak pokazał w 1994 roku Peter Shor, obliczenia kwantowe pozwalają zredukować złożoność problemu znajdowania okresu funkcji z  problemu wykładniczego w funkcji ilości bitów danej liczby do problemu wielomianowego klasy BPQ (Dodatek B). Fakt ten jest głównym źródłem zagrożenia związanego z kryptoanalizą kwantową.

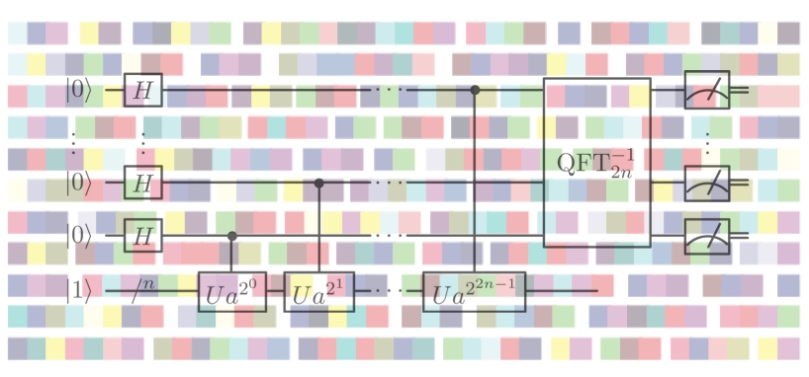
W optymalnej konfiguracji, Algorytm Shora dla przypadku z kluczem n-bitowym wymaga rejestru kwantowego zawierającego 2n+3 kubity logiczne. Dla algorytmu RSA-2048 są to więc 4099 kubity logiczne. Jednakże, z uwagi na błędy występujące w fizycznych realizacjach komputerów kwantowych, konieczne jest stosowanie rozbudowanych systemów kwantowej korekcji błędów. Zastosowanie korekcji błędów wymaga użycia co najmniej pięciu fizycznych kubitów do zakodowania jednego kubitu logicznego. Absolutnie minimalna liczba fizycznych kubitów, potrzebnych do przeprowadzenia kwantowej kryptoanalizy algorytmu RSA-2048 na komputerze kwantowym, jest więc rzędu 20 000. W praktyce jednak, konieczne może się okazać wykorzystanie dużo większej ilości kubitów pomocniczych, co może zwiększyć tę liczbę do setek tysięcy lub nawet milionów kubitów. Równie ważną kwestią jest osiągnięcie odpowiednio długiego czasu koherencji, gdyż realizacja powyższego algorytmu będzie wymagać przynajmniej 10⁷ kroków obliczeniowych.

Oszacowane powyżej wielkości mogą wydawać się zupełnie abstrakcyjne z perspektywy dostępnych dzisiaj możliwości przeprowadzania obliczeń kwantowych. Dla przykładu, najbardziej zaawansowany komputer kwantowy firmy Google posiada 53 kubity i jest w stanie wykonać kilkanaście kroków obliczeniowych. Jednakże, przyjmując hipotetyczny wykładniczy charakter rozwoju technologii kwantowych (analogiczny do prawa Moore’a), osiągnięcie poziomu miliona kubitów jest realne w perspektywie 30 lat. Załóżmy, że skala czasowa podwojenia ilości kubitów w procesorze kwantowym będzie wynosiła około 2 lata (podobnie jak obecnie ma to miejsce w przypadku liczby tranzystorów w procesorach klasycznych). W takim przypadku, w kolejnych latach możemy prognozować wartości: 100 (2021), 200 (2023), 400 (2025), 800 (2027), 1600 (2029), 3200 (2031), 6400 (2033), 12800 (2035), 25600 (2037), 51200 (2039), 102400 (2041), 204800 (2043), 409600 (2045), 819200 (2047), 1638400 (2049), … . Zgodnie z tą naiwną ekstrapolacją, poziom milionów kubitów powinien zostać osiągnięty do roku 2050. Istnieją również bardziej optymistyczne prognozy, wskazujące na możliwość nawet podwójnie wykładniczego rozwoju technologii kwantowych („prawo” Neven’a).

W kontekście kryptoanalizy, warto przywołać także przypadek funkcji skrótu (ang. hash functions), które są nieodzownym elementem współczesnych protokołów kryptograficznych.  Do najpowszechniejszych z nich należą: MD4, MD5, SHA-1, SHA-2 i SHA-3. Kryptoanaliza siłowa funkcji skrótu jest zasadniczo podobna do przypadku kryptografii symetrycznej i opiera się na wykorzystaniu algorytmu Grovera. W przypadku SHA-3 ze skrótem 512 bitowym, odporność na tzw. preimage attack jest więc na poziomie algorytmu symetrycznego z kluczem 256 bitowym. Tego samego poziomu jest odporność na ataki kolizyjne. Z uwagi na tę niepodatność na kryptoanalizę kwantową, funkcje skrótu rozpatruje się jako jeden z najbardziej obiecujących komponentów tak zwanej kryptografii postkwantowej.

Kryptografia postkwantowa

Kryptografia postkwantowa [2] jest odpowiedzią na potencjalne zagrożenie związane z  kryptoanalizą kwantową algorytmów klasycznej kryptografii asymetrycznej. Z uwagi na to, że kwantowe przyśpieszenie wykładnicze (Dodatek A) nie występuje w przypadku problemu przeszukiwania przestrzeni klucza, nie istnieją obecnie podstawy do obaw o bezpieczeństwo silnych algorytmów kryptografii symetrycznej, takich jaki AES-256, czy też algorytmów opartych na funkcjach skrótu.

Potencjalne zagrożenie związane z kwantową kryptoanalizą algorytmów kryptografii asymetrycznej nie może jednak zostać zbagatelizowane. Nawet jeśli kwantowe możliwości obliczeniowe umożliwiające kryptoanalizę RSA z kluczem 2048 bitowym pojawią się dopiero za 30 lat, należy podejmować działania zapobiegawcze. Po pierwsze, wynika to z faktu, że proces wdrażania (standaryzacja i implementacja) nowych rozwiązań kryptograficznych jest długotrwały, wymagając zarówno prac badawczych, szeroko zakrojonych testów podatności na kryptoanalizę, jak i samej implementacji w ramach istniejących systemów informatycznych. Po drugie, wiele zaszyfrowanych informacji pozostaje wrażliwymi przez okres kilkudziesięciu lat. Ich przechowywanie (jako szyfrogramy) i odszyfrowanie w momencie pojawienia się odpowiednich możliwości obliczeniowych, może doprowadzić nawet do ogólnoświatowego kryzysu. Dla przykładu, dostępne publicznie mogą stać się dane osobowe, transakcje bankowe, dane medyczne milionów osób, co otworzy szereg możliwości działań natury przestępczej.  Ponadto, zgodnie z Art. 25 ustawy z dnia 22 stycznia 1999 r. o ochronie informacji niejawnych: „Informacje niejawne stanowiące tajemnicę państwową podlegają ochronie, w sposób określony ustawą, przez okres 50 lat od daty ich wytworzenia.” Biorąc pod uwagę możliwość wykorzystania algorytmów kryptografii asymetrycznej do przetwarzania tego typu informacji (chociażby poprzez wykorzystanie kryptografii asymetrycznej do wymiany klucza), realność kryptoanalizy kwantowej w perspektywie 30 lat stawia pod znakiem zapytania bezpieczeństwo przetwarzanej obecnie informacji niejawnej, stanowiącej tajemnicę państwową.

Z uwagi na zagrożenia powyższego typu, w 2016 roku amerykański Narodowy Instytut Standaryzacji i Technologii (NIST) ogłosił program opracowania standardu kryptografii postkwantowej, odpornego na kryptoanalizę kwantową. Proces ten przebiega na zasadzie konkursu, podobnie jak to wcześniej miało miejsce np. w przypadku standardu AES. Obecnie, w drugiej rundzie, rozważana jest pula  26 propozycji. W pierwszej rundzie, z początkowych 250 zgłoszeń wybranych zostało 69 najbardziej obiecujących rozwiązań. Cały proces ma zostać zakończony do roku 2022. Rozpatrywany wachlarz rozważanych algorytmów kryptografii postkwantowej jest szeroki.  Do najbardziej obiecujących kierunków należą zaś:

• Algorytmy kratowe (ang. lattice-based cryptography)
• Algorytmy  oparte na kodach korekcyjnych (ang. code-based cryptography)
• Kryptografia wielu zmiennych (ang. multivariate cryptography)
• Podpis elektroniczny opary o funkcje skrótu (ang. hash-based signatures)

Z uwagi na subtelną naturę rozwiązań kryptograficznych, standaryzacja jest kluczowym elementem poprzedzającym szeroką implementacji nowych algorytmów. Etap ten  jest długotrwały i powiązany jest z badaniem odporności danych rozwiązań na ataki kryptologiczne. Należy mieć jednak na uwadze to, że nawet pomyślne wyłonienie nowego standardu nie gwarantuje późniejszego długotrwałego  bezpieczeństwa. Wiązać się to może zarówno z odkryciem niezauważonych wcześniej słabości rozwiązań, z pojawieniem się nowych schematów ataków oraz nowymi możliwościami obliczeniowymi. Dla przykładu, zaprojektowany na zlecenie NIST i stosowany od połowy lat siedemdziesiątych ubiegłego wieku symetryczny szyfr DES (z kluczem efektywnie 56 bitowym), okazał się możliwy do złamania już po 20 latach od jego wprowadzenia.

Fakt iż, możliwości kryptoanalizy szyfrów kryptografii postkwantowej są wciąż stosunkowo słabo poznane, istnienie realna obawa, że nawet wyłonione w procesie standaryzacji rozwiązania będą podatne na pewne typy ataków. Dlatego też, w początkowej fazie implementacji wydaje się zasadne opieranie się w jak największym stopniu na dobrze zbadanych elementach obecnych systemów kryptograficznych, takich jak funkcje skrótu lub kody korekcyjne. 

O ile proces standaryzacji prowadzony przez NIST jest w toku, w ramach niezależnych projektów podano już pewne rekomendacje co do algorytmów kryptografii postkwantowej. W szczególności, europejski projekt  PQCRYPTO, finansowany w ramach programu Horyzont 2020, rekomendował AES-256 i  Salsa20 z kluczem 256 bitowym jako postkwantowe algorytmy kryptografii symetrycznej. Dla kryptografii asymetrycznej, rekomendowany został natomiast szyfr McEliece’a, będący przykładem algorytmu opartego na kodach korekcyjnych [3]. 

Certyfikowana kwantowa przypadkowość

Jednymi z komponentów systemów kryptograficznych, mającymi fundamentalne znaczenie z punktu widzenia bezpieczeństwa,  są generatory liczb losowych. W praktyce, są to generatory liczb pseudolosowych, co na przykład w przypadku szyfrów strumieniowych (wykorzystywanych np. do zabezpieczania  transmisji w telefonii komórkowej) jest własnością pożądaną. Jednakże, już w przypadku generowania kluczy (będących ciągami bitów) oczekujemy niepowtarzalnej przypadkowości. Dotyczy to zarówno kluczy wykorzystywanych w kryptografii symetrycznej, jak i asymetrycznej.

Błędy w implementacji generatorów pseudolosowych mogą istotnie wpłynąć na obniżenie bezpieczeństwa, wykorzystujących je algorytmów kryptograficznych. Znanym przykładem jest wykazanie istnienia „tylnej furtki” w generatorze pseudolosowym Dual_EC_DRBG. Ujawnione przez Edwarda Snowdena informacje na temat programu deszyfrażu Bullrun, sugerują, że obecność furtki mogło być  działaniem celowym amerykańskiej National Security Agency (NSA) [4].  O ile więc furtki takie mogą być wprowadzane celowo przez agencje dbające o bezpieczeństwo publiczne, ich obecność stwarza również możliwość wykorzystania przez osoby, instytucje i państwa nieprzyjazne. 

Probabilistyczna natura mechaniki kwantowej stwarza atrakcyjną możliwość budowy generatorów losowych. Co więcej, rozwiązania takie są już dostępne komercyjnie.  Jednakże, otwarte zostaje potencjalne zagrożenie związane z wykorzystaniem  możliwych „tylnych furtek” w tego typu rozwiązaniach. Dlatego też, dąży się do opracowania rozwiązań które będą gwarantowały zarówno losowość, jak i niepodatność na ataki, zarówno na poziomie sprzętu, jak i oprogramowania.

Jednym z pojeść do tego zagadnienia jest wykorzystanie trudności obliczeniowej problemu przewidzenia rozkładu prawdopodobieństwa pomiarów dla odpowiednio dużych pseudolosowo-generowanych obwodów kwantowych. Własność tę można wykorzystać do generowania certyfikowanych kwantowo losowych ciągów binarnych (ang. certified quantum randomness) [5]. Losowość otrzymanego ciągu bitów jest zagwarantowana złożonością obliczeniową problemu przewidzenia z jakim prawdopodobieństwem dany ciąg może zostać wygenerowany przez obwód kwantowy. Ponadto, nawet kiedy źródło generatora obwodów zostałoby upublicznione, wygenerowane wartości losowe zachowają prywatność.

Metoda ta może być pomyślnie stosowana już z wykorzystaniem dostępnych obecnie komputerów kwantowych, posiadających kilkadziesiąt (zaszumionych) kubitów fizycznych. Dowodem na to jest niedawny rezultat otrzymany za pomocą komputera kwantowego opracowanego przez firmę Google. Rozważane zagadnienie próbkowaniem (ang. sampling), które przeprowadzono na 53 kubitowym procesorze może zostać zaadoptowane do zapewnienia certyfikowanej kwantowej przypadkowości [6].

Zastosowanie certyfikowanej kwantowej generacji kluczy może istotnie wzmocnić bezpieczeństwo zarówno konwencjonalnej kryptografii (asymetrycznej i symetrycznej) jak i algorytmów kryptografii postkwantowej. Jest to przykład rozwiązania hybrydowego w którym wykorzystuje się połączenie znanych i możliwych do zastosowania algorytmów kryptografii klasycznej z najnowszymi osiągnięciami w obszarze obliczeń kwantowych.

Kwantowa dystrybucja klucza

Nawet jeśli jest to możliwe w niepraktycznie dużych skalach czasowych, algorytmy kryptografii klasycznej, z wyłączeniem szyfru z kluczem jednorazowym (ang. one-time pad), są zawsze możliwe do złamania. Mechanika kwantowa dostarcza jednakże teoretycznie niepodatnej na kryptoanalizę metody szyfrowania informacji.  Opracowywaniem tego typu rozwiązań zajmuje się kryptografia kwantowa.

Kwantowa dystrybucja klucza (ang. quantum key distribution – QKD) [7] jest, rozważaną w ramach kryptografii kwantowej,  metodą bezpiecznego przesyłania sekretnego klucza za pośrednictwem stanów kwantowych pojedynczych fotonów. Metoda ta wykorzystuje kwantowe własności mikroświata (w szczególności, tak zwane twierdzenie o  zakazie klonowania kwantowego) do przesyłania informacji. Ponieważ przepustowość wykorzystywanych do QKD tzw. kanałów kwantowych nie dorównuje tym osiąganym w klasycznych łączach światłowodowych oraz radiowych, łącza kwantowe wykorzystywane są obecnie do przesyłania sekretnych kluczy, pozwalających zaszyfrować (klasyczną) wiadomość, nie zaś do transmisji samej wrażliwej informacji.  Udostępniony, za pośrednictwem QKD, klucz może być wykorzystany do zaszyfrowania danych np. z użyciem silnego symetrycznego szyfru AES-256.

Kwantowa dystrybucja klucza jest rozwiązaniem,  które zostało już wdrożone do komercyjnego użytku.  Jednakże, dostępne obecnie rozwiązania posiadają jedno kluczowe ograniczenie. Mianowicie, jest to dystans, na który możemy przesłać zabezpieczoną kwantowo informację. Wiąże się to z tłumieniem fotonów w światłowodzie i koniecznością stosowania skomplikowanych tzw. powielaczy kwantowych. Obiecującym rozwiązaniem tego problemu jest przesyłanie fotonów z zakodowaną kwantowo informacją poprzez atmosferę oraz przestrzeń kosmiczną. Udane próby międzykontynentalnej QKD z wykorzystaniem kwantowych technologii satelitarnych udało się przeprowadzić w 2017-tym roku. Obecnie trwają prace nad kilkoma projektami satelitarnymi, które mają na celu rozwój kwantowych technologii związanych z łącznością satelitarną. 

Połączenie światłowodowej oraz satelitarnej łączności kwantowej może pozwolić urzeczywistnić idę tzw. internetu kwantowego – niepodatnego na kryptoanalizę kanału wymiany informacji.  Stworzenie podwalin dla internetu kwantowego to m.in. jeden z filarów, rozpisanego na okres dziesięciu lat (2018-2028), flagowego programu Komisji Europejskiej – Quantum Flagship. Ponadto, w ramach projektu OPENQKD (Open European Quantum Key Distribution Testbed) powstaje obecnie w Europie eksperymentalna sieć do kwantowej dystrybucji klucza, której jeden z węzłów znajdzie się również w Polsce.

Warto w tym miejscu podkreślić, że systemy do kwantowej dystrybucji klucza, choć teoretycznie bezwarunkowo bezpieczne, mogą stać się jednak przedmiotem ataków. Istnieje mianowicie szerokie spektrum możliwych ataków fizycznych, wykorzystujących błędy w implementacji systemów do QKD. Jedną z prób rozwiązania tego problemu jest opracowanie algorytmów kryptografii kwantowej gwarantujących bezpieczeństwo w wymianie informacji, niezależne do wad implementacji fizycznych. Konieczne są jednakże dalsze prace zarówno teoretyczne, jak i eksperymentalne w tym obszarze.

Podsumowanie

Infosfera stała się kluczowym elementem współczesnej aktywności ludzkiej. Jej dynamiczny rozwój doprowadził jednak do pojawienia się zagrożeń zupełnie nowego typu. Dotyczy to zarówno poziomu jednostek, jak i społeczeństw. W konsekwencji, cyberprzestrzeń stała się równoprawnym do wody, lądu, powietrza i przestrzeni kosmicznej, obszarem działań wojennych. Powaga problemu doprowadziła do szerokiego zaangażowania państw i organizacji w obszarze zapewnienia bezpieczeństwa w cyberprzestrzeni. W Polsce, ważnym krokiem stało się sformułowanie w 2015 roku Doktryny Cyberbezpieczeństwa Rzeczypospolitej Polskiej [8]. Elementem realizacji jej założeń jest konsolidacja polskich zasobów  w obszarze cyberbezpieczeństwa i kryptologii w ramach utworzonego w 2019 roku Narodowego Centrum Bezpieczeństwa Cyberprzestrzeni (NCBC), funkcjonującego wcześniej jako Narodowe Centrum Kryptologii (NCK).

Technologie kwantowe, które coraz odważniej wychodzą z obszaru badawczego do fazy wdrożeń, stanowią zarówno potencjalne zagrożenie dla cyberbezpieczeństwa, jak i dają narzędzie dla jego wzmocnienia do bezprecedensowego poziomu. Zagrożenie związane jest głównie z możliwością kryptoanalizy algorytmów kryptografii asymetrycznej (w szczególności RSA i ECC). Natomiast, silne algorytmy kryptografii symetrycznej pozostaną odporne na kryptografię kwantową. W mojej ocenie, realistyczna wydaje się możliwość kryptoanalizy algorytmu RSA z kluczem 2048 bitowym w perspektywie czasowej 30 lat. Warto również mieć na uwadze prawdopodobieństwo opracowania nowych algorytmów, które mogą znaleźć zastosowanie w kryptoanalizie kwantowej.

Odpowiedzią na zagrożenie związane z kryptoanalizą kwantową jest kryptografia postkwantowa. Zadaniem które sobie stawia jest opracowanie algorytmów kryptografii z kluczem publicznym, niepodatnych na ataki kwantowe. W toku jest proces standaryzacji algorytmów kryptografii postkwantowej, po zakończeniu którego (około roku 2023) można spodziewać intensyfikacji w implementacji tego typu rozwiązań. Należy jednak zdawać sobie sprawę z faktu, że algorytmy kryptografii postkwantowej wciąż wymagają testów pod kątem kryptoanalizy, zarówno konwencjonalnej, jak i kwantowej.

Z drugiej strony, technologie kwantowe otwierają obiecującą możliwość implementacji rozwiązań kryptografii kwantowej. Jednym z nich jest kwantowa generacja klucza. Rozwiązania takie stają się możliwe do urzeczywistnienia z wykorzystaniem opracowywanych obecnie komputerów kwantowych. W perspektywie nadchodzącej dekady, certyfikowane kwantowe generowanie kluczy pozwoli wzmocnić bezpieczeństwo kryptografii klasycznej, jak również algorytmów postkwantowych. Kolejnym, bardzo obiecującym, rozwiązaniem dostarczanym przez kryptografię kwantową jest kwantowa dystrybucja klucza. Naziemna i satelitarna sieć kanałów kwantowych (tzw. kwantowy internet) pozwoli na bezwarunkowo bezpieczne przekazywanie sekretnych kluczy. Z ich pomocą, możliwe będzie  późniejsze przesyłanie informacji kanałami klasycznymi, stosując silne szyfry symetryczne.

Budowa infrastruktury do komunikacji kwantowej, która ostatecznie zapewni nowy poziom bezpieczeństwa w przesyle informacji jest zadaniem niezwykle złożonym i wymagającym integracji wielu zasobów i kompetencji. Jej utworzenie wykreuje zupełnie nowe realia dla cyberbezpieczeństwa. Warto w tym kontekście zaznaczyć, że z uwagi skomplikowaną naturę systemów do komunikacji kwantowych i kryptografii kwantowej, ważnym elementem będzie proces szkolenia specjalistów, którzy będą w stanie analizować subtelności stosowanych rozwiązań i przewidywać możliwość występowania nowych zagrożeń.

Przeprowadzona tu analiza jedynie zarysowuje zagadnienie cyberbezpieczeństwa kwantowego, akcentując podstawowe możliwości i zagrożenia. Dalsza szersza dyskusja, łącząca płaszczyzny: polityczną, akademicką, militarną i przedsiębiorczą, jest konieczna w celu wypracowania optymalnych rozwiązań, które pozwolą na wykorzystanie technologii kwantowych do zapewnienia jeszcze wyższego poziomu cyberbezpieczeństwa w Polsce i na świecie.   

Dodatek A – Kwantowy elementarz

Technologie kwantowe tworzy obecnie szerokie spektrum rozwiązań, wykorzystujących kwantową naturę mikroświata, opisywaną przez mechanikę kwantową. Do najważniejszych przykładów należą: systemy przetwarzania informacji kwantowej (komputery kwantowe),  systemy łączności kwantowej (oparte o kryptografię kwantową) i  systemy metrologii kwantowej (np. kwantowe magnetometry).   

Szczególną klasą układów kwantowych, odgrywają kluczową rolę w kwantowym przetwarzaniu informacji, są kubity. Kubity można postrzegać jako kwantowe odpowiedniki klasycznych bitów, mogące występować w kwantowych superpozycjach stanów „0” i „1”. Sytuacja robi się jeszcze ciekawsza kiedy rozważamy wiele oddziałujących ze sobą kubitów. Właśnie takie złożenie kubitów stanowi rejestr komputera kwantowego, na którym, poprzez wykonywanie odpowiednich operacji (unitarnych), przeprowadzane są obliczenia kwantowe. Wyzwaniem związanym z budowaniem tego typu maszyn jest odseparowanie rejestru kwantowego od środowiska zewnętrznego, które zaburza jego kwantową naturę. Wyzwaniem jest również odpowiednie kontrolowanie kubitów i przeprowadzanie na nich operacji. Przez wiele lat, fizycy zmagali się z osiągnięciem odpowiedniego poziomu koherencji kwantowej i sterowalności rejestrów kwantowych. Przełomowe okazało się wykorzystanie nadprzewodzących kubitów, które ostatecznie doprowadziło do eksperymentalnego wykazania przewagi (w wczasie obliczeń) komputera kwantowego nad najsilniejszym dostępnym superkomputerem klasycznym. Udało się to ostatecznie wykazać firmie Google, dla problemu próbkowania ciągów binarnych z zadanym przez obwód kwantowy  rozkładem prawdopodobieństwa [6].

Trudność w emulowaniu obliczeń kwantowych na komputerach klasycznych wiąże się z faktem, że stan układu n kubitów opisywany jest w 2ⁿ wymiarowej przestrzeni Hilberta. W konsekwencji, na przykład by opisać układ 100 kubitów należy użyć wektora posiadającego około 10³⁰ składowych. Próba zapisania takiego wektora zarówno w obecnych jaki i możliwych do wyobrażenia przyszłych komputerach klasycznych jest praktycznie skazana na niepowodzenie.  Z drugiej strony, operowanie w 2ⁿ wymiarowej przestrzeni Hilberta,  dysponując n kubitami umożliwia wykonywanie wykładniczo rosnącej z n liczby operacji. Na własności tej opiera się tzw. paralelizm kwantowy, mogący w pewnych przypadkach doprowadzić do kwantowego przyśpieszenia wykładniczego (ang. exponential speed-up) w rozwiązaniu pewnych problemów. Z sytuacją taką spotykamy się, w szczególności, w przypadku algorytmu faktoryzacji Shora, znajdującym zastosowanie w kryptoanalizie kwantowej.

Dodatek B – Złożoność obliczeniowa 

Złożoność obliczeniowa, w uproszczeniu określa poziom trudności rozwiązania danego problemu.  Dla przykładu, rozważmy problem znalezienia konkretnego elementu w nieuporządkowanym zbiorze N elementowym. Element taki znajdziemy w średnio N/2 próbach. Czas potrzebny na znalezienie elementu będzie więc skalował się liniowo wraz z liczebnością (mocą) zbioru. Jest to przykład problemu należącego do wielomianowej klasy złożoności – P (ang. Polynomial). Innym  przykładem problemu należącego do klasy P jest mnożenie liczb.

Nie wszystkie znane problemy należą jednak do kasy P, a przynajmniej tak się wydaje. Okazuje się mianowicie, że istnieje cały szereg problemów dla których nie udało się, jak dotąd, zaproponować algorytmów ich rozwiązywania które należałyby do klasy P. Problemy takie określamy mianem NP (ang. Nondeterministically Polynomial). Są to takie problemy dla których znając wynik możemy w czasie wielomianowym zweryfikować czy propozycja wyniku jest rozwiązaniem czy też nie. Przykładem takiego problemu, jest rozkład liczby złożonej na czynniki pierwsze (problemu faktoryzacji). Problemy klasy NP znajdują szerokie zastosowanie w kryptologii. Otwartym i jednym z najważniejszych problemów matematycznych jest odpowiedzenie na pytanie czy faktycznie NP≠P?

Uogólnienie rozważań do obliczeń kwantowych wymaga wprowadzenia nowych klas złożoności. Na potrzeby tego artykułu, wprowadzimy jedynie klasę BQP (ang. bounded-error quantum polynomial time). Do klasy tej należą problemy, dla których istnieje możliwość znalezienia rozwiązania w czasie wielomianowym, z prawdopodobieństwem co najmniej 2/3 (czyli błędem nie większym niż 1/3). Okazuje się, że kwantowy algorytm Shora pozwala zredukować złożoność obliczeniową problemu faktoryzacji, klasycznie klasyfikowanego jaki problem wykładniczy, do takiej właśnie złożoności. Jest to przykład kwantowego przyśpieszenia wykładniczego.

Bibliografia

[1] M. Mosca,  Cybersecurity in an Era with Quantum Computers: Will We Be Ready? IEEE Security & Privacy, September/October 2018, pp. 38-41, vol. 16
[2] D. J. Bernstein, T. Lange,  Post-quantum cryptography, Nature, 549(7671), 188-194.
[3] PQCRYPTO – Post-Quantum Cryptography for Long-Term Security. Initial recommendations of long-term secure post-quantum systems
[4] D. J. Bernstein, T. Lange, R. Niederhagen, Dual EC: A Standardized Back Door. In: Ryan P., Naccache D., Quisquater JJ. (eds) The New Codebreakers. Lecture Notes in Computer Science, vol 9100. Springer, Berlin, Heidelberg
[5] Acín, A., Masanes, L. Certified randomness in quantum physics. Nature 540, 213–219 (2016).
[6] Arute, F., Arya, K., Babbush, R. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019)
[7] A. Shenoy-Hejamadi, A. Pathak, S. Radhakrishna, Quantum Cryptography: Key Distribution and Beyond, Quanta 2017; 6: 1–47
[8] Doktryna Cyberbezpieczeństwa Rzeczypospolitej Polskiej, 2015.

                                                                                                                               © Jakub Mielczarek

Artykuł został opublikowany na portalu CyberDefence24.